菲涅耳方程：他们是什么？（衍生和解释）|mabetx官网电气4U.

内容

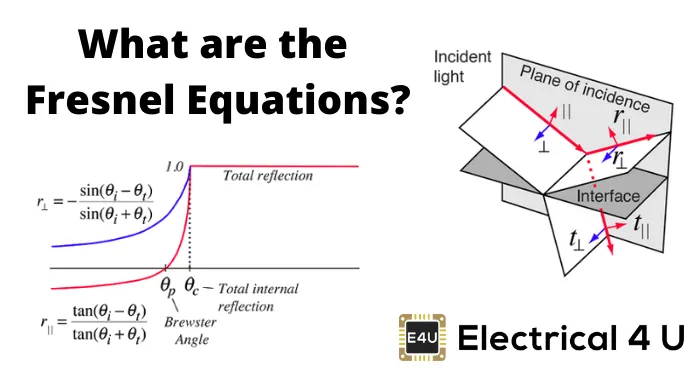
什么是菲涅耳方程？

菲涅耳方程(也称为菲涅耳系数)被定义为电场反射和传输波到事件波的电场。该比率是复杂的，因此描述了相对幅度以及波之间的相位偏移。

菲涅耳方程(菲涅耳系数)描述了光入射到两种不同介质之间的界面时的反射和透射。菲涅耳方程是由奥古斯丁-让·菲涅耳提出的。他是第一个明白光是横波的人。

当光入射在电介质的表面上时，它将作为入射角的函数反射和折射。反射波的方向由“反射法则”给出。

常规生活中可以看到菲涅耳效应。它可以在闪亮和粗糙的表面上看到。水面上的这种效果非常清晰。当从空气介质中入射在水的光时，光线将根据入射角反射。

菲涅耳效应无处不在。如果您尝试环顾四周，您会发现很多示例。这种影响高度取决于发病率。

入射角是您正在寻找的物体的视线和表面之间的角度。下图显示了事件的角度在菲涅耳反射中的效果。

S和P极化

具有入射辐射的表面法线和传播矢量的平面称为入射面或入射面。

发病率平面在入射光极化的反射强度中起重要作用。偏振被定义为横波的属性，其指定振荡的几何取向。

两极分化有两种类型;

S-Polarization
P-Polarization

当光的偏振垂直于入射平面时，这种偏振称为s偏振。“S”这个词来自德语Senkrecht.这意味着垂直。S偏振也称为横向电气（TE）。

当光的偏振平行于入射的平面或其躺在事件的平面中时。该平面被称为p偏振。S偏振也称为横向磁性（TM）。

下图表明入射光在S偏振和P偏振中反射和传输。

菲涅耳方程复杂折射率

菲涅耳方程是一个复杂的等式，意味着它考虑了幅度和相位。菲涅耳方程在除了电力之外考虑相位的电磁场复振幅而言。

这些方程是电磁场的比率，它有不同的形式。复振幅系数用r和t表示。

反射系数r是反射波的电场复振幅与入射波的比值。反射系数t是透射波与入射波的电场复幅值之比。

如上图所示，我们假设入射角是θ_一世，反映在θ的角度_R.，并以θ的角度传输_T.。

N_一世入射光和N的介质的折射率是多少_T.是透射光介质的折射率。

因此，有四个菲涅耳方程;反射系数r的两个方程_P.和r_S.)和反射系数t的两个方程，即(t_P.和t_S.)。

菲涅耳方程推导

让我们假设入射光反射，如上图所示。在第一种情况下，我们将推导出S偏振的菲涅耳方程。

对于S偏振，平行分量E和垂直组件B在两个介质之间的边界上连续。

因此，由边界条件，我们可以写出e场和b场的方程，

（1） $\begin{equation*}E_i + E_r = E_t\end{equation*}$

（2） $\ begin {arearation *} b_i \ cos（\ theta_i） - b_r \ cos（\ theta_r）= b_t \ cos（\ theta_t）\ neg {arequation *}$

我们用下面B和E之间的关系来消去B。

$\ [b = \ frac {ne} {c_0} \]$

从反思法中，

$\theta_i = \theta_r$

将此值放在EQ-2中，

（3） ${方程*}\ \开始压裂{n_i E_i} {c_0} \ cos (\ theta_i) - \压裂{n_i E_r} {c_0} \ cos (\ theta_i) = \压裂{n_t E_t} {c_0} \ cos (\ theta_t) \{方程*}结束$

（4） $\ begin {arearation *} n_i \ cos（\ theta_i）[e_i - e_r] = n_t e_t \ cos（\ theta_t）\ neg {arequation *}$

（5） ${方程*}n_i \ \开始因为(\ theta_i) [E_i - E_r] = n_t [E_i + E_r] \ cos (\ theta_t) \{方程*}结束$

（6） $\{方程*}开始n_i E_i \ cos (\ theta_i) - n_i E_r \ cos (\ theta_i) = n_t E_i \ cos (\ theta_t) + n_t E_r \ cos (\ theta_t) \{方程*}结束$

（7） $n_i E_i cos(\theta_i) - n_t E_i cos(\theta_t) = n_t E_r cos(\theta_t) + n_i E_r cos(\theta_i) \end$

(8) $\ begin {arearation *} e_i [n_i \ cos（\ theta_i） - n_t \ cos（\ theta_t）] = e_r [n_t \ cos（\ theta_t）+ n_i \ cos（\ theta_i）] \ neg {arequation *}$

(9) $\{方程*}开始r_s = \压裂{E_r} {E_i} = \压裂{n_i \ cos (\ theta_i) - n_t \ cos (\ theta_t)} {n_t \ cos (\ theta_t) + n_i \ cos (\ theta_i)} \{方程*}结束$

现在，对于反射系数T，来自EQ-1和EQ-4，

（10） ${方程*}n_i \ \开始cos (\ theta_i) [E_i - (E_t - E_i)] = n_t E_t \ cos (\ theta_t) \{方程*}结束$

（11） $\ begin {arearation *} n_i \ cos（\ theta_i）[2e_i - e_t] = n_t e_t \ cos（\ theta_t）\ neg {arequation *}$

(12) $\ begin {arearation *} 2e_i n_i \ cos（\ theta_i） - e_t n_i \ cos（\ theta_i）= n_t e_t \ cos（\ theta_t）\ end {arequation *}$

(13) $begin{equation*} 2E_i n_i \cos(\theta_i) = E_t n_i \cos(\theta_i) + n_t E_t \cos(\theta_t) \end{equation*}$

(14) $\ begin {arearation *} t_s = \ frac {e_t} {e_i} = \ frac {2 n_i \ cos（\ theta_i）} {n_i \ cos（\ theta_i）+ n_t \ cos（\ theta_t）} \ nod {方程式*}$

这些是垂直偏振光（S偏振）的菲涅耳方程。

现在，让我们推出平行偏振光（P偏振）的方程。

对于S偏振，E场和B场的方程是;

(15) $\开始{方程*}E_i \ cos (\ theta_i) + E_r \ cos (\ theta_i) = E_t \ cos (\ theta_t) \{方程*}$

(16) $\ begin {arearation *} b_i - b_r = b_t \ end {arequation *}$

我们用下面B和E之间的关系来消去B。

$\ [b = \ frac {ne} {c_0} \]$

(17) $(begin{equation*}n_i E_i - n_i E_r = n_t E_t) \end{equation*}$

$n_i [E_i - E_r] = n_t E_t$

$\ [\ frac {n_i} {n_t} [e_i - e_r] = e_t \]$

把这个值放到eq-15中，

(18) ${方程*}E_i \ \开始cos (\ theta_i) + E_r \ cos (\ theta_i) = \压裂{n_i} {n_t} [E_i - E_r] \ cos (\ theta_t) \{方程*}结束$

(19) $\ begin {arearation *} n_t [e_i \ cos（\ theta_i）+ e_r \ cos（\ theta_i）] = {n_i} [e_i - e_r] \ cos（\ theta_t）\ end {arequation *}$

（20） $\ begin {arearation *} n_t e_i \ cos（\ theta_i）+ n_t e_r \ cos（\ theta_i）= n_i e_i \ cos（\ theta_t） - n_i e_r \ cos（\ theta_t）\ end {arequation *}$

（21） $\{方程*}开始n_t E_i \ cos (\ theta_i) - n_i E_i \ cos (\ theta_t) = -n_t E_r \ cos (\ theta_i) - n_i E_r \ cos (\ theta_t) \{方程*}结束$

（22） $\{方程*}开始E_i [n_t \ cos (\ theta_i) - n_i \ cos (\ theta_t)] = -E_r [n_t \ cos (\ theta_i) + n_i \ cos (\ theta_t)] \{方程*}结束$

（23） $\ begin {arearation *} e_i [n_i \ cos（\ theta_t） - n_t \ cos（\ theta_i）] = e_r [n_t \ cos（\ theta_i）+ n_i \ cos（\ theta_t）] \ neg {arequation *}$

（24） $\{方程*}开始r_p = \压裂{E_r} {E_i} = \压裂{n_i \ cos (\ theta_t) - n_t \ cos (\ theta_i)} {n_t \ cos (\ theta_i) + n_i \ cos (\ theta_t)} \{方程*}结束$

现在，从eq-17得到反射系数t

$\ [n_i e_i - n_t e_t = n_i e_r \]$

$\ [e_i - \ frac {n_t} {n_i} e_t = e_r \]$

将此值放在EQ-15中

(25) $\ begin {arearation *} e_i \ cos（\ theta_i）+ [e_i - \ frac {n_t} {n_i} e_t] \ cos（\ theta_i）= e_t \ cos（\ theta_t）\ neat {arequation *}$

(26) $\ begin {arequation *} e_i \ cos（\ theta_i）+ e_i \ cos（\ theta_i） - \ frac {n_t} {n_i} {n_i} e_t \ cos（\ theta_i）= e_t \ cos（\ theta_t）\ neat {等式*}$

(27) $\{方程*}2开始E_i \ cos (\ theta_i) = \压裂{n_t} {n_i} E_t \ cos (\ theta_i) + E_t \ cos (\ theta_t) \{方程*}$

(28) $\ begin {arearation *} 2 e_i n_i \ cos（\ theta_i）= n_t e_t \ cos（\ theta_i）+ {n_i} e_t \ cos（\ theta_t）\ neg {arequation *}$

(29) $\ begin {arearation *} 2 e_i n_i \ cos（\ theta_i）= e_t [n_t \ cos（\ theta_i）+ {n_i} \ cos（\ theta_t）] \ end {arequation *}$

（30） $\{方程*}开始t_p = \压裂{E_t} {E_i} = \压裂{2 n_i \ cos (\ theta_i)} {n_t \ cos (\ theta_i) + {n_i} \ cos (\ theta_t)} \{方程*}结束$

让我们总结一下所有的四个菲涅耳方程，

$\ [r_s = \压裂{n_i \ cos (\ theta_i) - n_t \ cos (\ theta_t)} {n_t \ cos (\ theta_t) + n_i \ cos (\ theta_i)} \]$

$\ [t_s = \ frac {2 n_i \ cos（\ theta_i）} {n_i \ cos（\ theta_i）+ n_t \ cos（\ theta_t）} \]$

$\ [r_p = \ frac {n_i \ cos（\ theta_t） - n_t \ cos（\ theta_i）} {n_t \ cos（\ theta_i）+ n_i \ cos（\ theta_t）} \]$

$\ [t_p = \ frac {2 n_i \ cos（\ theta_i）} {n_t \ cos（\ theta_i）+ {n_i} \ cos（\ theta_t）} \]$