毕奥萨瓦尔定律是什么
的毕奥萨伐尔定律方程描述的是磁场由恒定的电流产生当前的。它将磁场与电流的大小、方向、长度和接近度联系起来。毕奥-萨伐尔定律与两者都是一致的安培全电流定律和高斯定理。毕奥萨伐尔定律是静磁学的基础,起着与静磁学相似的作用库仑定律在静电学。
毕奥萨伐尔定律是由两位法国物理学家,让·巴蒂斯特·比奥和费利克斯·萨瓦尔推导出的数学表达式磁通密度在1820年,由于附近的载流导体而产生的一点。通过观察磁性罗盘指针的偏转,这两位科学家得出结论:任何当前的元素都会向其周围的空间投射磁场。

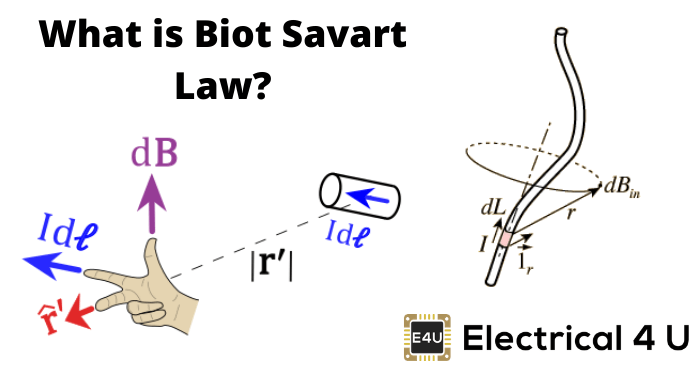
通过观测和计算,推导出一个数学表达式,这表明,磁通密度的dB, dl元素的长度成正比,目前的我,和θ角的正弦电流的方向和磁场的向量加入一个给定的点和当前元素和成反比的平方给定点的距离从当前元素,r。
毕奥萨伐尔定律的陈述与推导
的毕奥萨伐尔定律可以表述为:
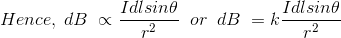
其中,k是一个常数,取决于所使用的介质和单位系统的磁性能。在国际单位制,
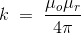
因此,最后的毕奥萨伐尔定律推导是,
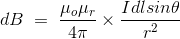
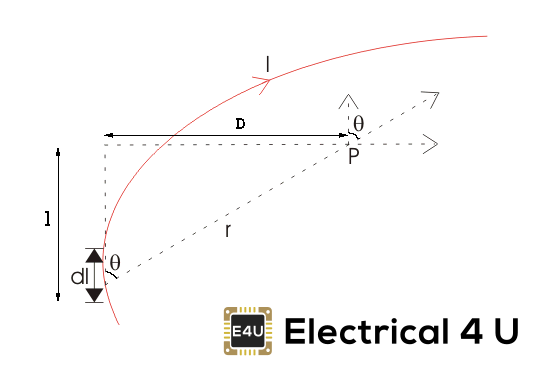
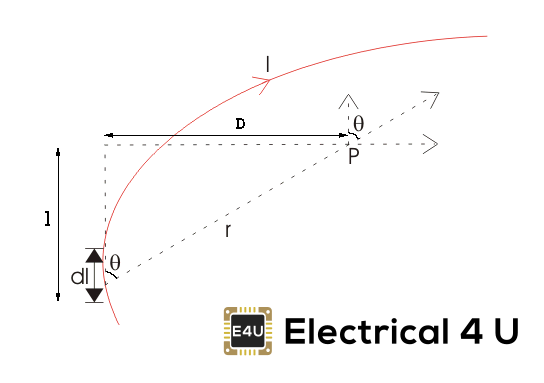
让我们考虑一根携带电流I的长导线,同时考虑空间中的一个点p。电线在下图中显示,用红色表示。我们也考虑到点P距离r处无限小的导线dl,如图所示。这里,r是一个距离矢量,在导线的无限小的部分,与电流方向成夹角θ。
如果你试着把这个情况形象化,你可以很容易地理解点P的磁场密度,因为无穷小长度的导线dl,与这部分导线所携带的电流成正比。
由于通过这条无限小长度的导线的电流等于整个导线本身的电流,我们可以这样写,
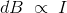
我们也可以很自然地认为,点P处的磁场密度,由无穷小长度的导线dl引起,与点P到dl中心的直线距离的平方成反比。数学上我们可以把它写成,
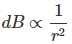
最后,磁场点P处的密度,由于导线无限小的部分,也与导线无限小的长度dl的实际长度成正比。
由于θ是距离矢量r与电流方向之间的夹角,因此直接垂直于点P的dl分量为θ中的dlsin,
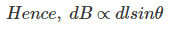
现在,结合这三个表述,我们可以这样写,
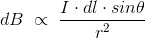
这是的基本形式毕奥萨伐尔定律
现在,把常数k(我们在本文开始时已经介绍过)的值放在上面的表达式中,我们得到
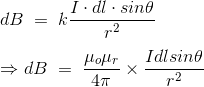
在这里,μ0用在常数k的表达式是绝对磁导率它的值是4π107Wb/ A-m是国际标准化组织的单位制。常数k的表达式的μr是相对渗透率的媒介。
现在,由载流总长度决定的P点的通量密度(B)导体或者电线可以表示为,
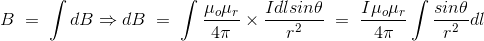

如果D是点P到导线的垂直距离,那么
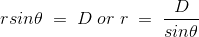
现在,P点的通量密度B的表达式可以改写为:
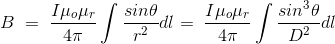
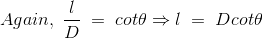
根据上图,
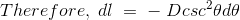
最后,B的表达式是,
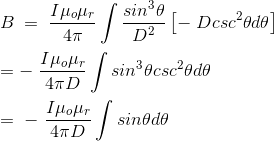
这个角θ取决于导线的长度和点p的位置。对于一定长度的导线,图中所示的角θ从θ1到θ2变化。因此,点P处的磁通密度由导体是,
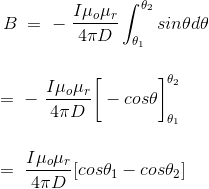
假设导线是无限长,那么θ将从0到π变化,即θ1= 0到θ2=π。把这两个值放在上面的最终表达式中毕奥萨伐尔定律我们得到了,
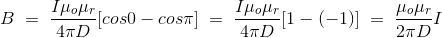
这只不过是表达安培定律。