主动低通滤波器：设计和应用|mabetx官网电气4U.

内容

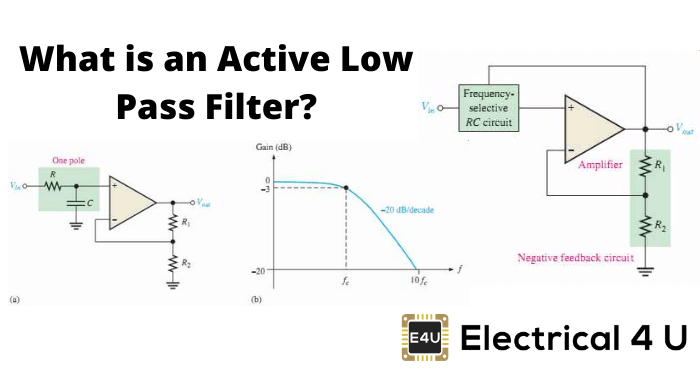
什么是有源滤波器?

一个主动过滤器是一种包含一个或多个的过滤器有源电路组件如晶体管或晶体管运算放大器(放大器)。它们从外部能量来源获得能量，并利用它来增加或放大信号输出。

操作放大器还可用于通过使滤波器的输出带宽通过产生更选择的输出反应来形成或改变电路频率响应。

OP-AMP具有高输入阻抗，低输出阻抗和其电压增益反馈回路由电阻器的混合物产生。有源滤波器，与仔细电路设计一起使用时，产生优异的性能特点，非常好的精度，陡峭的滚动和低噪音。

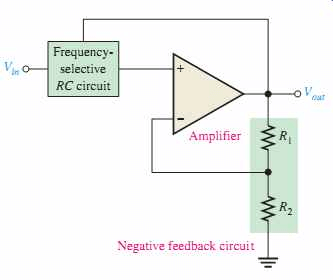
什么是有效的低通滤波器？

如果有源过滤器只允许低频分量并拒绝所有其他高频分量，则它被称为有效低通滤波器。有效的低通滤波器由OP-AMP组成。OP-AMP的输入是高阻抗信号，其产生低阻抗信号作为输出。

在设计有效低通滤波器时，放大器的性能起到了非常重要的因素。有两种主要的有源低通滤波器即开关电容类型和连续电容类型。过滤器可从一阶获得直到八阶设计。

除了通带之外，电路的频率响应与无源RC滤波器的频率响应相同电压增益增加输出信号的幅度。

通带从0Hz或DC开始，用于低通滤波器，并在-3DB上继续到指定的截止点。信号衰减超出切断频率。有效的低通滤波器根据过滤器的顺序进行分组。我们将讨论1^圣和2^nd订购有源低通滤波器。

低通滤波器的倒数是a高通滤波器，这允许具有高于截止频率的频率的信号，并阻止该截止频率以下的所有频率。还有带通滤波器，它结合了低通滤波器和高通滤波器的功能，只允许特定频率范围内的频率。

一阶有效低通滤波器

一种一阶有源低通滤波器是一种简单的滤波器，其仅由伴随有源组件OP-AMP伴随的一个反应性分量电容器组成。电阻器被使用电容器或电感器形成RC或RL低通滤波器。在无源电路中，输出信号幅度小于输入信号幅度。

为了超越这个问题，介绍了有源电路设计。当被动低通滤波器连接到OP-AMP时反相或非反相条件，它给出了一个有效的低通滤波器设计。简单的RC电路与单个OP-AMP的连接显示在下面的图像中。

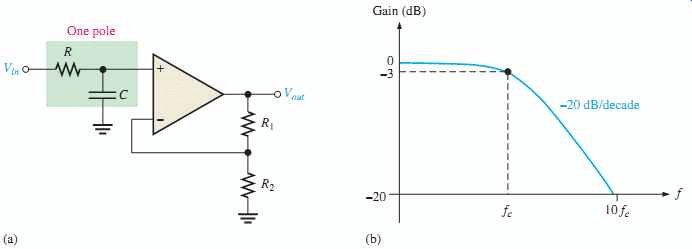
该RC电路有助于向放大器输入提供低频信号。放大器作为Unity增益输出缓冲电路操作。该电路已添加输入阻抗值。电路的OP-AMP具有非常低的输出阻抗值，这有助于为滤波器提供高稳定性。

与无源滤波器进行比较时，有源滤波器具有放大器设计为的布置电压跟随器(缓冲器)使直流增益为1的。这种配置为滤波器提供了良好的稳定性和高功率增益。这个过滤器的主要缺点是没有电压增益高于1，可以通过额外的电路设计进行整流。

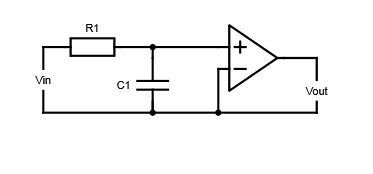
具有放大的第一阶有效低通滤波器

如上所述，上述滤波器设计不提供高于一的电压增益。因此，我们需要修改电路，如下所示。

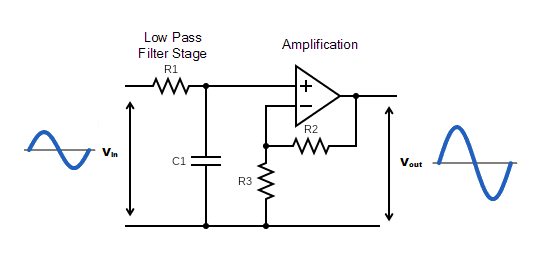
在较低频率时，输入信号直接通过放大电路。当输入频率增加时，它被旁通并通过电容c，这通过通带增益增加了输出信号的幅值。

在非反相放大器电路配置中，滤波器的电压增益的测量作为反馈电阻（R.₂）除以其相应的输入电阻（R_3.）价值。

$DC = 1 + \ FRAC {R_ {2}} {R_ {3}}$

一阶低主动通道滤波器反转配置

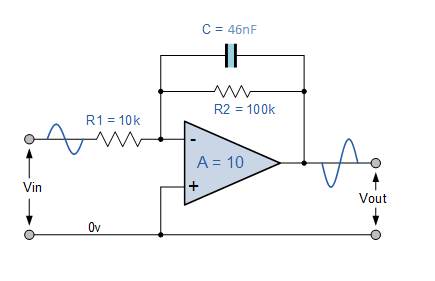
采用8引脚配置的运放IC741设计了反相低通滤波器。在反相模式下，运算放大器的输出与输入信号相差180度。最初，运放必须提供直流电源。直流功率的大小取决于信号在输出时被放大的大小。

输出是具有峰值峰值的AC信号。在这个例子中，我们将设计10增加10的电路，因此12VDC的电源电压提供给V⁺，运放引脚7和-12VDC供电给V^-OP-AMP的引脚4。这被称为反相运算放大器配置，输出信号将比输入信号反转。

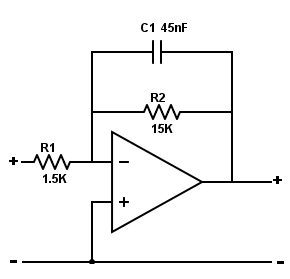
一阶低主动通道过滤器非反转配置

在此配置中，还使用IC741 OP-AMP。但是，这里输入信号和输出信号将相互相位。形成低通滤波器部分的RC是电路的前半部分。

然后，信号通过OP-AMP，其中信号通过与电阻器R2和R1成比例的电压增益而放大。在该配置中，外部阻抗对电容器的电抗没有影响，因此稳定性改善。

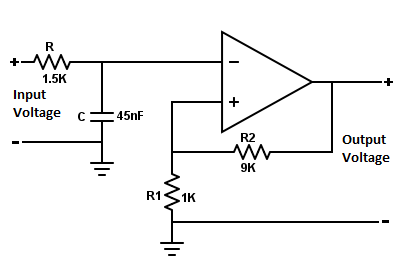
一阶低通滤波器电压增益

频率分量用于获得滤波器的电压增益。

$v电压\增益\(现代{})= \压裂{V_{出来}}{V_{在}}= \压裂{现代{F}}{\√6{1 + \离开(\压裂{F} {F c{}} \右)^ {2}}}$

哪里，

V._在是输入电压
V._出是输出电压
一种_F是过滤器的通带增益（1 + r₂/ R.₁）
f是赫兹输入信号的频率
F_C是赫兹的截止频率

当频率增加时，增益减少20 dB。可以从上述频率增益方程检查有效低通滤波器的操作。让f成为工作频率和f_C是截止频率。

在低频时

$\ begin {align *} \ frac {v_ {out}} {v_ {in}} = a_ {f} \ neg {align *}$

当工作频率等于切断频率时

${对齐*}\ \开始压裂{现代{f}} {\ sqrt{2}} = 0.707现代{f} \{对齐*}结束$

并且在高频

$\ begin {align *} \ frac {v_ {out}} {v_ {in}} <a_ {f} \ neg {align *}$

从上述方程可以看出，在低频时，电路的增益等于增益的最大值。而在高频条件下,电路的增益比最大增益Af非常小。当操作频率等于切断频率,增益等于0.707 Af。在这些滤波器电路,通带增益量化值(级)的表达分贝或D b这是电压增益的函数。

$现代{v} (dB) = 20 log_{10} \离开(V_{出}/ V_正确的{}\]$

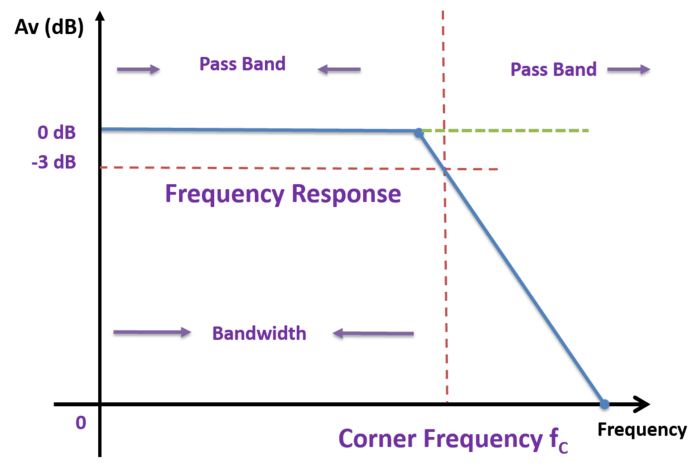
一阶活动低通滤波器传输功能

该转换功能又称系统功能或网络功能的控制系统。它表示为数学函数。当用于系统的频域分析时，它利用Laplace变换等变换方法。过滤器在信号频率上工作。

因此，使用频域的分析和图形描述是描述过滤器进行的最有效的仪器。因此，通常使用频域方程和增益与频率与频率与频率的曲线。

它需要他们的数学描述，以便系统的传递函数研究网络频域。电压传递函数是比例的拉普拉斯变换用于特定方案的输出和输入信号，如下所示。

$H (s) = \压裂{V_ {0} (s)} {V_{我}(s)}$

其中V0（S）和VI（S）是输出和输入电压，S是复杂的拉普拉斯变换变量。

通过连接电阻和电容器，设计了一个单极低通滤波器，用于低频应用，如下所示。

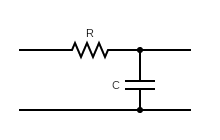
可以给出上述电路的传递函数

$H (s) = \压裂{1 / sC} {R + 1 / sC} = \压裂{1}{RcS + 1} = \压裂{1 / RC} {s + 1 / RC}$

现在，在上面的方程中，用它在频域中的等效值来代替拉普拉斯常数。

$| H（\ omega）| = \ FRAC {1 / RC} {J \ OMEGA + 1 / RC}$

传递函数的绝对值定义为幅度或volatge增益，可以表示如下所示

$| h（\ omega）| = | \ | \ frac {1} {rcs + 1} | = | \ frac {1} {JRC \ Omega + 1} | = \ FRAC {1} {\ SQRT {1 + RC（\omega）^ {2}}}}$

电阻等于电容器的阻抗的频率，据说是如下所示的临界频率。

$当r = \ frac {1} {\ oomega_ {c}} \ neg {align *}开始{aligne *} \ oomega = \ oomega_ {c}$

因此，

${\ omega_ {c}} = \ frac {1} {rc}$

在适当的取代后进入这个方程，我们得到了

$gain = | h（\ omega）= \ frac {1} {\ sqrt {1 +（\ oomega / \ oomega__ {c}）^ {2}}} = \ frac {1} {\ sqrt {1} {\ sqrt {1+（f/ f_ {c}）^ {2}}}}$

过滤器的相移由

$\ varphi = tan ^ { - 1} \ left（\ frac {\ omega} {\ omega_ {c}} \右）$

滤波器的切断频率和相移可以按如下方式计算

$f_ {c} = \ frac {1} {2 \ pi rc}$

$\ phi = tan ^ { - 1}（2 \ pi frc）$

当RC级级联在一起时，可以获得类似的滤波器配置。

一阶活动低通滤波器设计和示例

设计一个非反相有源低通滤波电路，低频增益为10，高频截止频率或角频率为175Hz，输入阻抗为20Kω。

提供非反相放大器的电压增益

$A_ {F} = 1 + \ FRAC {R_ {2}} {R_ {1}} = 10$

现在假设R1的值为1kΩ并从上述等式计算值R2。

$r_ {2} =（10-1）x r_ {1} = 9x \ time1k \ omega = 9k \ omega$

因此，对于10的电压增益，R1和R2的值分别为1kΩ和9kΩ。DB中的增益为20Loga = 20Log10 = 20dB

现在我们通过截止频率值为175Hz，输入阻抗值为20kΩ。通过代替这些值在方程中，并且C的值可以按如下计算。

$f_ {c} = \ frac {1} {2 \ pi rc}$

$c = \ frac {1} {2 \ pi rf_ {c}} = \ frac {1} {2 \ pi \ times 175 \ times 20k \ omega}$ = 45.47 nf

因此滤波器的最终设计及其等效频响曲线如下图所示。

有效低通滤波器电路

有效低通滤波器的典型电路如下：

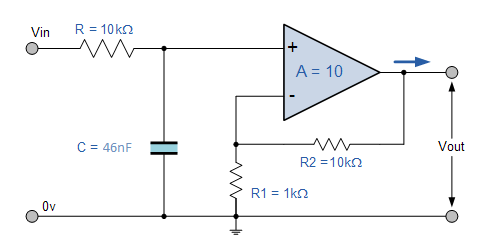
有效低通滤波器频率响应曲线

有源低通滤波器的频率响应曲线如下:

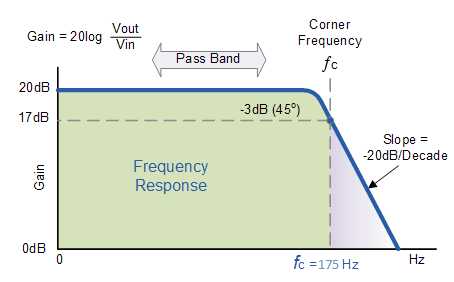
非反相放大器滤波器

简单的非反相放大器滤波器如下所示：

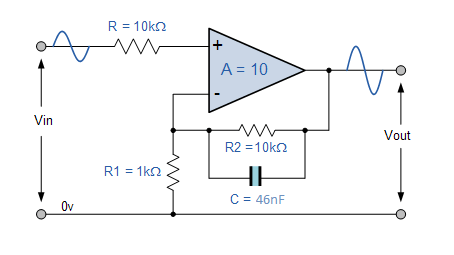
反相放大器过滤器

以下给出了等效的反相放大器滤波器：

等效 - inverting-电路 - 用于 - 问题 — 求解此问题的等效反相电路

二阶有效低通滤波器

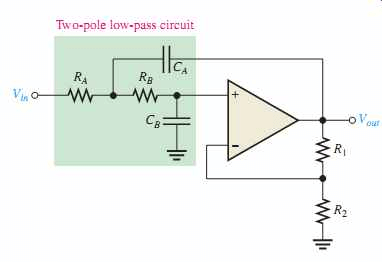
二阶滤波器也归因于VCVS滤波器，因为这里使用的OP-AMP是电压控制电压源放大器。这是应用中使用的另一个重要类型的主动滤波器。

除了停车带滚截止之外，二阶低通滤波器的频率响应是难以区分的，因为停滞滚动将是40dB /十年的一阶滤波器的两倍。因此，二阶电源低通滤波器的设计步骤是相同的。获得二阶滤波器的简单方法是级联两个一阶滤波器。

当滤波器电路级联时，滤波器的总增益等于每个阶段的产品。主动二阶（双极）过滤器是必不可少的，因为它们可用于设计高阶滤波器。具有订单值的过滤器可以通过级联和二阶滤波器来构建。

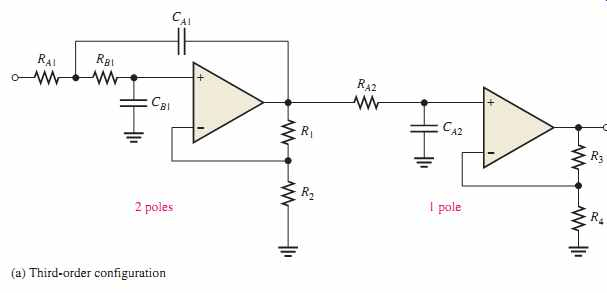
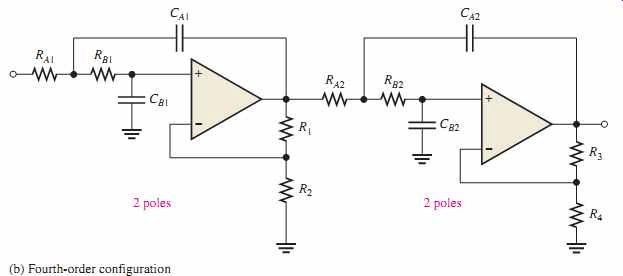
二阶电源低通滤波器电压增益

二阶滤波器的增益是将在一起的“N”级的增益的乘积。例如，如果级联两个一阶滤波器，则滤波器的增益将如下。

$\ begin {align *} a_ {v} = a_ {v1} \ times a_ {v2} \ neg {align *}$

$\ begin {align *} a_ {v} = 10 \ times 30 = 300 \结束{align *}$

如果在DB中给出了两个阶段的增益，那么通过添加两个增益来计算总增益

$\ begin {align *} a_ {v}（db）= a_ {v1} + a_ {v2} \ neg {align *}$

二阶电源低通滤波器截止频率

截止频率方程是给出的

$\ begin {aligne *} f_ {c} = \ frac {1} {2 \ pi \ sqrt {r_ {3} r_ {4} c_ {1} c_ {2}} \ {2}}} \ neg {align *}$

当R3 = R4 = R和C1 = C2 = C时，截止频率将被给出

$f_ {c} = \ frac {1} {2 \ pi rc}$

滤波器第一阶段的截止频率的增益为-3dB。对于二阶滤波器，组合两个第一阶滤波器的增益，总增益将为-6dB。

二阶电源低通滤波器设计和示例

假设Rs1 = Rs2 = 15Kω，电容C1 = C2 = 100nF。增益电阻为R1=1Kω，R2= 9Kω，R3 = 6Kω，R4 =3Kω。根据这些规格设计一个二阶有源低通滤波器。

截止频率为

$\ begin {align *} f_ {c} = \ frac {1} {2 \ pi rc} \ neg {align *}$

（1） $\ begin {aligne *} f_ {c} = \ frac {1} {2 \ pi \ times 15 \ times 10 ^ {3} \ times 100 \ times 10 ^ {-9}} \ end {alight *}$

$\ begin {aligne *} f_ {c} = 106.10Hz \结束{align *}$

一级放大器的增益为

$\ begin {aligne *} a_ {1} = 1 +（r_ {2} / r_ {1}）\结束{align *}$

$\{对齐*}开始现代{1}= 1 + \压裂{9 \ * 10 ^{3}}{1 \ * 10 ^{3}}{对齐*}\结束$

$\ begin {aligne *} a_ {1} = 10 \结束{align *}$

第二级放大器的增益是

$\{对齐*}开始现代{2}= 1 + (R_ {4} / R_{3})结束\{对齐*}$

$\ begin {aligne *}α_{2} = 1 + \ FRAC {6 \ times 10 ^ {3}} {3 \ times 10 ^ {3}} \ end {align *}$

$\begin{align*} A_{2} =3 \end{align*}$

过滤器的总增益

$\ begin {align *} a_ {v} = 10 \ times 3 \ END {align *}$

$\ begin {align *} a_ {v} = 30 \ end {align *}$

DB中的总增益

（2） $\ begin {align *} a_ {v} = 20 log（30）\ end {align *}$

（3） $\ begin {align *} a_ {v} = 30db \ neg {align *}$

截止频率增益为

（4） $\ begin {aligne *} \ gain \在f_ {c} = 30db -6db = 24db \ neg {align *}$

主动低通滤波器应用

这些过滤器主要用于电子应用程序，如扬声器和低音炮。它们充当扬声器中的过滤器，并作为低音炮的输入。它们还在音频放大器和均衡器设计中发挥着重要作用。当您使用模拟到数字转换器时，这些过滤器用作抗锯齿滤波器来控制信号。当涉及声学和声音时，滤波器用于停止从发射声音来阻止高频信号以防止回波。

汽车音频应用中的主动滤波

运算放大器是汽车音频电路最流行的施工块之一。为了提升音频效率，许多开发人员选择将OP-AMP集成到汽车音频电路中。有源滤波器消除了对音频信号的不期望干扰的可能性。过滤对于帮助为汽车的音频系统提供高质量的声音是必不可少的。

具有运算放大器或有源滤波器的过滤器，同时放大音频信号，保留频率响应。另一种流行的Op-AMP过滤器在汽车音频系统中使用适用于整个车辆的不同频率范围，适用于各个扬声器。然而，驱动大型超低炮所需的能量，特别是在更大的卷，可能会损害更大的频率扬声器。HPF和LPF可用于设置截止频率，以提供频率的右扬声器。

用于生物医学应用的主动低通滤波器

用于低电压和低能量，ECG监控系统应用中，采用两级运放拓扑的有源CMOS LPF。这种米勒补偿两级放大器可用于低功耗、低电压、高共模抑制比(CMRR)的应用，如生物医学工具和小型电池驱动设备，如心脏起搏器、心电图(ECG)，在这些地方低功耗是主要关注的问题。

有源低通滤波器:设计与应用

什么是有源滤波器?

什么是有效的低通滤波器？

一阶有效低通滤波器

具有放大的第一阶有效低通滤波器

一阶低主动通道滤波器反转配置

一阶低主动通道过滤器非反转配置

一阶低通滤波器电压增益

一阶活动低通滤波器传输功能

一阶活动低通滤波器设计和示例

有效低通滤波器电路

有效低通滤波器频率响应曲线

非反相放大器滤波器

反相放大器过滤器

二阶有效低通滤波器

二阶电源低通滤波器电压增益

二阶电源低通滤波器截止频率

二阶电源低通滤波器设计和示例

主动低通滤波器应用

汽车音频应用中的主动滤波

用于生物医学应用的主动低通滤波器

留下你的评论取消回复