磁场可以是永磁的,也可以是电磁铁的。两个磁场都储存了一些能量。永磁体总是创造磁通它不受其他外部因素的影响。但是电磁体产生可变磁场的基础是多少当前的它携带。这个电磁铁的尺寸决定了磁场的强度,也决定了储存在这个电磁铁中的能量。
首先,我们认为磁场是由电磁铁,即一个由几个电磁铁组成的线圈引起的。转弯。这个线圈或电感器当它通过a连接时携带的电流是I吗电池或电压源通过一个开关。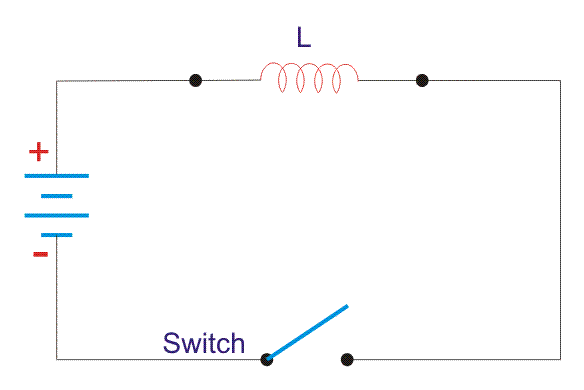
假设电池电压是V伏,电感的值是L亨利,电流I将在稳定状态下流动。
当开关接通时,电流就会从零流向其稳定值。但是由于自感,一个感应电压出现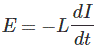
这个方向总是和电流的变化率相反。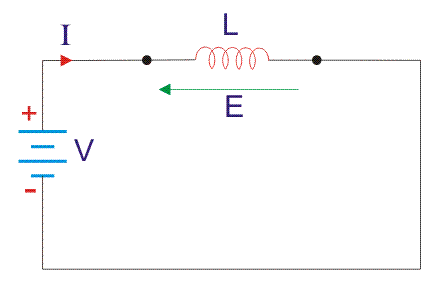
这里,电流通过电感器所做的能量或功是U。
当电流从零值开始并与感应电动势E反向流动时,能量将从零值逐渐增加到U。
dU = wdt,其中W是小的幂,W = - i
所以,电感中储存的能量是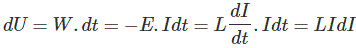
现在对能量从0到它的最终值进行积分。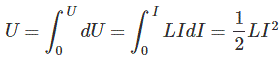
再一次,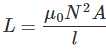
根据线圈的尺寸,其中N是线圈的匝数,A是线圈的有效横截面积,l是线圈的有效长度。
再一次,
式中,H为磁化力,N为线圈匝数,l为线圈有效长度。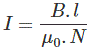
现在把L和I的表达式放到U的方程中,我们得到新的表达式,即。
因此,在电磁场即导体中储存的能量可以从其尺寸和磁通密度来计算。
现在让我们开始讨论由于永磁体而储存在磁场中的能量。
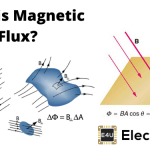
总计通量通过磁体的横截面面积A为φ。
φ= B.A,其中B为通量密度。
现在这个通量φ有两种类型,(a)φr这是磁铁的剩余磁通和(b)φd这是消磁通量。
所以,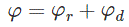
根据磁通量守恒定律。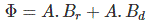
再次,Bd=μ。H,这里H是磁通量强度。
现在可以从磁体的H和尺寸计算出磁动势或磁动势。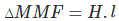
其中l是两极之间的有效距离。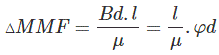

现在,为了计算能量,我们必须首先考虑磁通路径。
磁体内部用于退磁的磁阻路径记为R米,
和
现在W米,是储存在磁铁内部磁阻中的能量。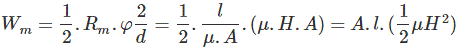
现在能量密度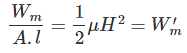
看看下面的模型。虚线框是磁体和一个磁阻路径Rl因为机械负载是通过磁铁连接的。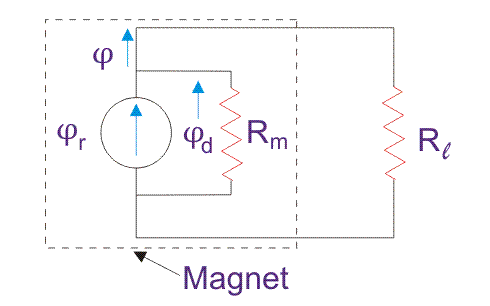
现在应用节点方程和循环方程,我们得到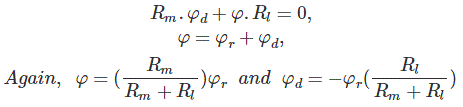
现在,如果我们在磁场中做任何机械功,那么能量需要W。
同样,如果我们在永磁体附近放置一个电磁线圈,这个线圈就会受到一个力。要移动这个线圈需要做一些功。这个能量密度是关于永磁体和线圈磁体的共能。永磁体和线圈的磁通强度分别为H和HC。
这个共能表示为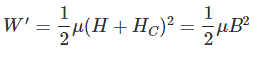
式中,B为永磁体附近线圈位置的磁通密度。