Wien桥振荡器：电路和频率计算

什么是wien桥振荡器？

一个维恩桥振荡器是一种类型的相移振荡器基于Wien桥网络（图1A），包括以桥式方式连接的四个臂。这里两个臂纯力电阻，而另外两个臂是一种组合电阻器和电容器。特别是，一臂具有串联连接的电阻器和电容器（R₁和c₁）而另一个并行有它们（r₂和c₂）。这表明网络的这两个武器的行为与之相同高通滤波器或者低通滤波器，模仿图1B所示的电路的行为。

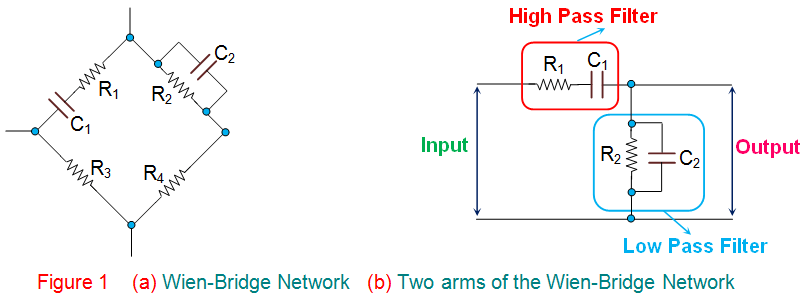
在该电路中，在高频下，电容器的电抗C₁和c₂将少得多电压V._0.将变为零作为r₂将被短缺。接下来，在低频下，电容器C的电抗₁和c₂会变得非常高。

但是，即使在这种情况下，输出电压V_0.将仅保持零，因为电容器C₁将充当开路。Wien桥网络展示的这种行为分别在低频率和高频的情况下使其成为引线滞后电路。

Wien Bridge振荡器频率计算

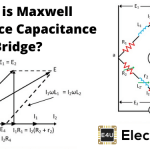
然而，在这两个高频率和低频中，存在特定的频率抵抗性并且电容电抗将相互等于，产生最大输出电压。该频率被称为谐振频率。使用以下公式计算Wein Bridge振荡器的谐振频率：

此外，在此频率下，输入和输出之间的相移将变为零，输出电压的大小将变得等于输入值的三分之一。此外，可以看出，Wien-Bridge仅在这种特定频率上平衡。

如果是Wien-Bridge振荡器，图1的Wien桥接网络将用于反馈路径，如图2所示。使用BJT的Wein振荡器的电路图（双极结晶体管）如下所示：

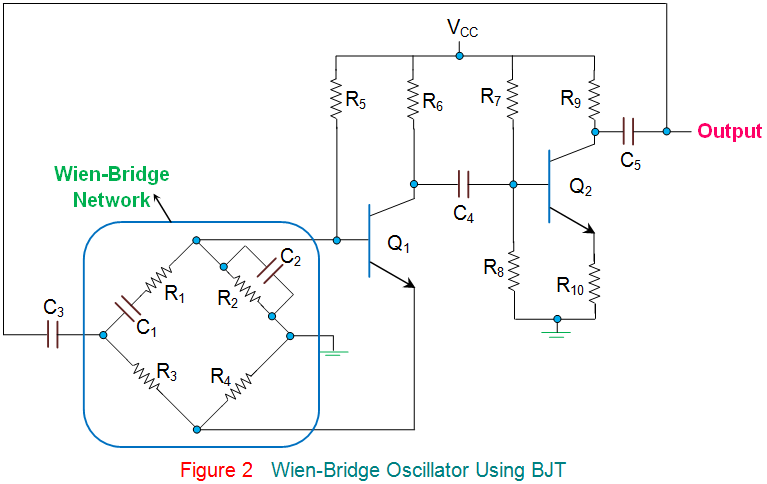
在这些振荡器，放大器部分将包括由此形成的两级放大器晶体管，问：₁问：₂，其中Q的输出₂作为输入的输入被返回给q₁通过Wien-Bridge网络（在图中的蓝色机箱内显示）。这里，电路中固有的噪声将导致基座的变化当前的问：₁在以180的相移扩增后，它将出现在收集点。^O.。

这被馈送为Q的输入₂通过C._4.并进一步放大，出现在180的额外相移^O.。这使得向维恩桥网络馈送到360的信号的净相位差^O.，满足相移标准以获得持续振荡。

然而，这种情况将仅在谐振频率的情况下满足，因此在频率方面，维也纳桥振荡器将是高度选择的，导致频率稳定设计。

Wien-Bridge振荡器甚至可以使用OP-AMPS.作为其放大器部分的一部分，如图3所示。然而，应注意，在这里，当Wien-Bridge网络提供零相移时，需要运算放大器作为非反相放大器。此外，从电路中，显而易见的是，输出电压被反馈到反相和非反相输入端。

在谐振频率下，施加到反相和非反相终端的电压将相等且相互相同。然而，即使在此，放大器的电压增益也需要大于3以启动振荡并等于3以维持它们。一般来说，这些基于OP-AMPWien Bridge振荡器由于它们的开环增益对它们的限制，不能以上操作1 MHz以上。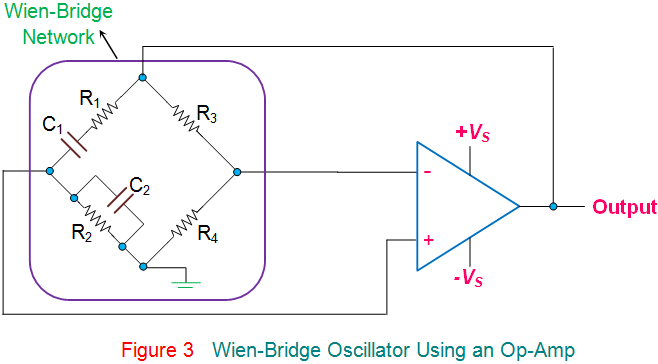

Wien-Bridge网络是低频振荡器，用于在20Hz至20kHz之间产生音频和子音频频率。此外，它们提供稳定的，低扭曲的正弦输出在各种频率范围内，可以使用十几年电阻箱选择。此外，这种电路中的振荡频率可以很容易地变化，因为它只是需要变化电容器C₁和c₂。然而，这是其中的振荡器需要大量的电路元件，并且只能运行到某个最大频率。